Category: novel chronology

7.2 Horologium Augusti, Ara Pacis

AbbreviATIONS
EXPLANATIONS

We know from Pliny the Elder that in Rome on the Field of Mars (Campus Martius), the erection of an Obelisk (shipped from Heliopolis, Egypt in 10BC) was finished in BC9.

In January BC9, near the obelisk, the shrine Ara Pacis Augustae (Altar of Peace of Augustus) was completed, too.

Another name for the above Obelisk, including its supposed sundial function, is Horologium Augusti or Solarium Augusti (the Solarium of Augustus). The obelisk is a “gnomon” (vertical shadow-caster) whose possible various functions are partly disputed today. According to Pliny, it was not only the obelisk itself that served as a shadow caster on the pavement of the Field of Mars. The shadow of a gilded bronze sphere, the “gilt ball” (aurata pila) mounted by a rod on the “pyramidion” (small pyramid) at the top of the obelisk played an important role, too.

Emperor Augustus dedicated his obelisk to the God Sun, Latin “SOL”.

You can watch the almost 5-minute video of Professor Bernard Frischer and his fellow researchers about the simulated antique Mars field.

The obelisk collapsed in the 9th or 10th century, was buried, and was found in 1512. In 1789, it was re-erected in Piazza Montecitorio (south of its original location), where it is still on display today (that is why now known mainly as the Montecitorio Obelisk.) The restored Ara Pacis is also not on display in its original location but in a new museum in Rome, built especially for the reconstructed version.

The two monuments were not only built at the same time but are also linked in other ways. One of these links is the topographic alignment of the two objects, namely, the sides of them are axially turned to each other. When I refer to both “objects” simultaneously, I will call the pair of Horologium Augusti and Ara Pacis together briefly as the “HAAP” in this blog.

The way any gnomon works is that the peak of its shadow virtually draws lines on the horizontal surface, as shown in the figure below.

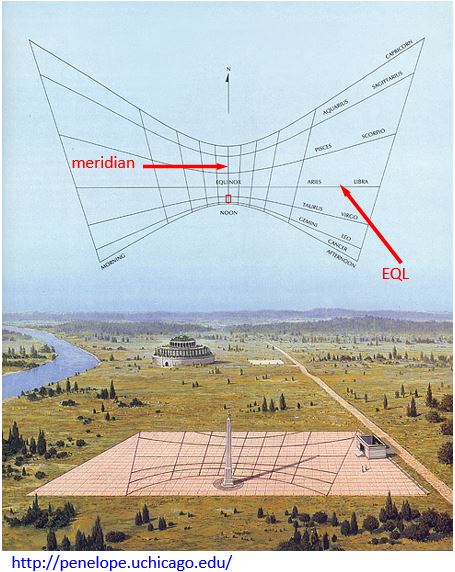
Exactly at local noon, the middle of the shadow line of the obelisk itself shows from South to Nord along the meridian, the line running S-N across the vertical axis of the obelisk in the horizontal base plane. The direction of the obelisk’s shadow shows the local noontime on each day of the year as usual by gnomonical instruments. Using the sphere’s shadow, the meridian markings can indicate the sun’s position every noon of the year. On the day of the equinoxes (VEQ and AEQ), the shadow of the gilded sphere follows the so-called equinoctial line (EQL, perpendicular to the meridian line) along the West-East direction from sunrise to sunset.

Based on the above facts, the functions usually assigned to Horologium Augusti and Ara Pacis (HAAP) are the following:

  • Meridian function
  • Equinoctial function
  • Sundial function
  • AEQ-birthday function

Meridian function:

According to the experts, the length of the shadow at noon, i.e., the position of the shadow of the gilded sphere indicated the day of the year, or more precisely, mainly seasonal time boundaries during the year, like the weather- and wind- changings. The shortest shadow belongs to the longest daylight of the year at Summer Solstice (SUS), and the longest shadow belongs to the shortest daylight of the year at Winter Solstice (WIS). In 1980, the renowned German archaeologist Edmund Buchner found bronze gravings in the antique pavement marking the meridian. Due to this archaeological find of Buchner, the obelisk’s “meridian function”, which is virtually a “noon sundial function”, became certain.

Due to the height of the obelisk, the length position of the spherical shadow on the meridian changed on the calendrical VEQ and AEQ day of the successive years. This change happened in a cycle of four years. The measure of the change was sufficient so this made the Horologium Augusti a suitable instrument to show and prove the correctness of the four-year leap year cycle of Caesar’s new calendar. However, the change in shadow length remained in a narrow band at noon on VEQ day and AEQ day of the different years.

Equinoctial function:

Because of the existence of the theoretical equinoctial line EQL (which is virtually a narrow equinoctial band if we examine many years), some researchers state that the days of the equinoxes (VEQ and AEQ days) were also indicated by the west-to-east tracing of the shadow of the obelisk’s gilded sphere, from sunrise to sunset, along the EQL. There is no historical record or archaeological evidence of this equinoctial function. No equinoctial signs like the meridian signs in the antique pavement have been found on the Field of Mars.

Sundial function:

Pliny did not write about a sundial. However, following the opinion of Edmund Buchner, the obelisk is generally considered a colossal sundial (Horologium, solarium) with a horizontal clock face. Buchner based this partly on earlier opinions and partly on his own considerations. Buchner’s hypothesis is logical because gnomons were often used as a sundial. However, no ancient descriptions or archaeological evidence of a complete sundial function (according to the above image) has yet been found on the Field of Mars.

AEQ-birthday function:

According to Buchner, the obelisk and the Ara Pacis were not only built but also designed together and functionally linked to form a “cooperating architectural ensemble”.

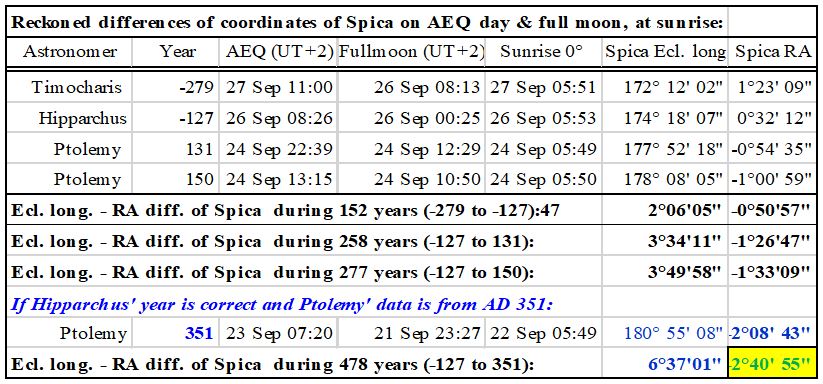
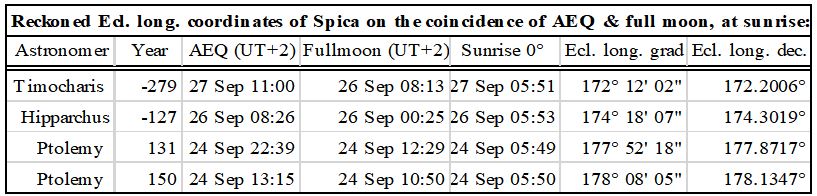
Buchner considered one of the main tasks of the obelisk to be to cast the shadow of the golden sphere on the altar of Ara Pacis on the day of the AEQ, which was the same as the birthday of Emperor Augustus, 23 September. According to Buchner, this could symbolise that the emperor’s mission from birth (natus ad pacem) was to establish peace. But Buchner did not know in 1976-1980 exactly on which day AEQ fell in BC9!

Namely, in BC9, the AEQ fell on 25 September and therefore did not coincide with the birthday of Emperor Augustus, as we have already seen!

According to a recent Astro-archaeological digital simulation (Prof. Bernard Frischer et al.), on 23 September 9BC, the sun was still so high that the obelisk’s shadow was too short, so it could not reach the western opening of Ara Pacis, let alone the altar. A few minutes later, when the shadow was longer and could have got the “door”, the shadow had veered more off the opening and turned south, moving to the south outside wall of the entrance.

So, Buchner’s AEQ-birthday function did not work in BC9!

However, on 25 September BC9, the day of the AEQ, the shadow of the golden sphere could already reach the threshold of the Ara Pacis too. But even on this AEQ-day, the shadow did not reach even the western sidewall of the altar table.

It is a fact that the EQL topologically points towards the altar of Ara Pacis. Indeed, on the day of AEQ, the shadow of the golden sphere moved along the EQL towards the western entrance and altar of Ara Pacis.

For me, based on astronomical considerations, this means the following: 

The spatial position of the AEQ, as seen from the earth, is stable, resulting in relatively stable Sun lights directions on the AEQ days of every year. The required shadow angle of incidence occurs on the AEQ day of each year. Even the corresponding shadow length produced on the AEQ day of each year shows only a slight length difference.

On the AEQ day of different years, the time of occurrence of a given shadow direction changes year by year only with some minutes. The variation in the shadow length associated with the AEQ day falls within a narrow interval in different years. If the Horologium were still stable standing today, the shadow length of Obelisk would fall within this narrow band even on the present AEQ day. I have verified these facts by Stellarium calculations, which are not detailed here.

In my view, 
the Obelisk-Ara Pacis complex was designed and built 
to be strongly linked to the AEQ day. 
(In an astronomical and not calendrical sense). 
We will see in the next blog how "special" 
the Horologium many years long functioned 
on the astronomical day of AEQ. 
The day of AEQ fell not in 9BC but, 
as we have already shown, 220 years later, in 212CE, 
on the calendrical and at the same time 
on the astronomical birthday of Emperor Augustus.

7. KEY EVENTS of ROMAN EMPIRE

AbbreviATIONS
EXPLANATIONS

I have selected seven major historical events from the Roman period after Caesar’s reign, from the era of the best documented Western Roman Empire (WRE). I examine how the dates of these events would fit astronomically if they had occurred 220 years later than we accept today.

Widely known events have been chosen. Perhaps the only exception is the story and examination of the Horologium Augusti. I will analyse Augustus’ sundial because it has been the subject of much research and has vast literature. However, as far as I see, no complete interpretation has been made of the “light-shadow cooperation” of Augustus’ Obelisk and Ara Pacis.

Historical events selected to study their date:

7.1 Birthday Feast of Augustus (from 212CE instead of 9BC)

7.2 Horologium Augusti, Ara Pacis (from 212CE instead of 9BC)

7.3 New Date for Jesus’ Birth (214CE instead of 7BC)

7.4 Solar Eclipse and Augustus’ Death (234CE instead of AD14)

7.5 New Date of Jesus’ Crucifixion (256CE instead of AD33)

7.6 The Coptic Paradox (Coptic Church AD284, Diocletian 504CE)

7.7 The First Council of Nicaea (545CE instead of AD325)

Let us take a time trip around the marble buildings of the antique Rome in the following posts.

6. SUBTOTAL

AbbreviATIONS
EXPLANATIONS

Based on described a new sketch of the overall picture of AD time has been put together. With another symbolism, the current image of the magic Hungarian Rubik cube suggests that the cube can be assembled.

It is, therefore, worth pausing briefly to look back at the sketch and its associated core findings from a slightly more distant perspective.

It had already been established by several independent amateur researchers (hardly influenced by outside interests) that there is probably (they believe with certainty) a 200-300 year inserted, historically fictitious period in AD time. I agree that as a period of continuous chronology, the entire Roman history could “merely in principle” be pushed back along the time axis.

In contrast to earlier theories, I claim such insertion of a “long period” could occur only during the “Dark Middle Ages”. If there is such an inserted period, I state, it must lay between the fall of Rome (476 AD) and the life-years of the Venerable Bede (e.g., Bede’s year, 725 AD). This finding has shortened the length of the theoretically insertable “historical time gap” to a maximum of about 249-years.

I also think the years of the Ancient Greek Olympics and the AUC may have been mistakenly synchronised with the result of Dionysius Exiguus. This synchronisation was not done by Exiguus but was retroactively calculated by historians. Exiguus had only calculated a “year distance”, presumably based mainly on the indiction cycles. I do not consider it impossible that the retrospective Easter tables compiled by Bede are faking.

We have found a replacement for 45BC, the currently accepted starting year of Julius Caesar’s calendar reform. The year AD176, which is 220 years later, fits calendrically and astronomically better than BC45. The 220-year insertion also fits well with the 249-year permissible period mentioned above.

A single fitting is not enough to prove anything. So, we have also shown that the 220-years of insertion into history is astronomically feasible because the “backwards shifting” by 220 years is challenging to recognise retrospectively!

If 220 years are inserted, the Dark Ages are seemingly extended by 220 years, backwards in time. This “extending” obviously had a retroactive effect.

However, the retroactive effect is limited. The time shift could only have extended back to the time of Hipparchus because Hipparchus was already living in the astronomical sense at the time we are now assuming. The centuries after about the life-years of Hipparchus could therefore be “shrunk” by 220 years as the retroactive effect of the extension occurred later.

In my opinion, the above considerations and explanations might be sufficient to show that, in astronomical terms, the possibility of the insertion of 220 years cannot be ruled out.

If a historical event seems feasible, like the misinterpretation or falsification of chronology, we should investigate whether it actually happened or not.

Based on the above findings, we should analyse the effects of the hypothetical insertion of 220 years by focusing on the astronomical parameters of the dates of some selected historical and evangelical “key events”!

I will explore these issues in the following posts.

5.3.5 Shrinkage of Antiquity

AbbreviATIONS
EXPLANATIONS

It seems that a period was prolonged after the fall of the Western Roman Empire. But I can imagine that at the same time, an earlier period was also “pressed together”, like wine grapes… Of course, from this “pressed period” remained only its essence. Let us see why and how was it astronomically feasible to shrink an older period.

I have extended the insights of Thompson and the other scientists above as follows:

I have assumed that Ptolemy, or rather Hipparchus himself, converted the difference in celestial coordinates in general from RA to Ecl. long. coordinate. This assumption is justified because of 2° Ecl. long. is a better illustration of precession since 2° is precisely a “round fraction”, 1/180th of the total angular rotation of precession of 360° Ecl. long.

I also assumed that the 2°40′ difference for the period 128BC – AD131 (or AD131) described by Ptolemy “remained somehow” in RA coordinates.

Ptolemy had left by mistake the angular rotation 
of Spica in RA, 
or had deliberately changed it to RA. 
It is also possible that this data 
retroactively (even centuries later) have been transformed, 
by mistake or intentionally to RA. 
After all, the very important original works 
somehow "disappeared"!?

Ptolemy also wrote about the trigonometric transformability of celestial coordinates, for which Hipparchus developed the “chords” procedure. (Not incidentally, the genius Hipparchus is also the father of trigonometry.)

It is easy to find out today that 
the equivalent of 2°40' RA is 6°34' Ecl. long.
Obviously, an angular rotation of 6°34' Ecl. long. 
corresponds to a much longer period than 265 years. 
It results in around 480 years! 
Expressed in precession, this makes round:
1°/73 years angular velocity or 26.280 years cycle!
A reasonable approximation compared to today's parameters!
Not like the one attributed to Almagest
(min) 1°/100 years and (max) 36.000 years!

So, to continue our train of thought, let us accept that Hipparchus’ years are astronomically in their correct year. (Year of his measurement 128BC). This is also acceptable because Hipparchus’ years fit well into the (from Rome) independent early relative chronology of ancient Greek history before the Roman conquest, within which it could hardly be misinterpreted.

Let us also assume that Ptolemy’s “own” data came from a year of AEQ & full moon simultaneity. So, we temporarily accept as Ptolemy’s measurement year the previously proposed year AD131 instead of AD138.

The only year (after 128BC)
corresponds well to 6°34' Ecl. long.
precession angular rotation,
as well as the coincidence of AEQ & full moon, is:
AD351.

The recalculated angular rotation is
for the period 128BC - AD351:
2°40'55" RA = 6°37'01" Ecl. long.
It also follows that 2°40' RA was measured 
quite accurately in antiquity.
It appears that someone could have
"misinterpreted" 2°40' RA as Ecl. long. 
or changed it to Ecl. long!

Let us see all these in detail below:

Table 6. (Author’s calculations based on Stellarium.)

If the year of Hipparchus’ measurement (-127= BC128) is correct and the year of Ptolemy’s measurement was AD351 instead of AD131, as I had previously assumed, then Ptolemy’s real, original years have, for some reason, been shifted back precisely 220 years (from AD351 to AD131) along the time axis.

The Almagest dates from AD370, not from AD150!
The Era of Ptolemy has become due to 
backwards shifting closer in AD time
to the years of Hipparchus than it really was.
The time difference between Hipparchus and Ptolemy
has "shrunk" by 220 years.
This "shrinkage" may be due to the 
centuries later "extension" of an epoch 
by 220 years,as assumed in the current hypothesis.

I note that the “shrinking” of a long past period is more difficult to recognise retrospectively as the “extension” of a younger period. The original state is more difficult to reconstruct than it is in the case of the “stretching” of a later period.

If an old year (such as the year 128BC of Hipparchus) lies correctly in the AD system, then the insertion of an extended period (such as the 200 years of Hunnivári and the 247 years of Szekeres) must be accompanied by a shortening of an earlier period. The authors of these earlier theories do not mention the possibility of a similar shrinkage of an earlier period!

Following in the footsteps of Exiguus and Beda and accepting their data, later historians “quasi automatically” shortened the period of ancient Greek and Egyptian history before the Roman occupations. An earlier period of history in these regions had been compressed.

To mislead later historians, all that was needed was to “remove” the historical descriptions of some earlier “historical key events”, thus “erasing the past”. Only some old documents relating to Greek and Egyptian history had to be removed or destroyed. The removal and destruction had been “supported” by the serial and supposedly deliberate burning and then final destruction of the famous library of Alexandria (Musaeum) in the 7th century! Shortly before the period of forgery that I assume…

My note: Another possible way of solving the issue of precession objection is to assume that the era of Hipparchus and Timocharis was 220 years closer to the present as we date it now. In this case, we must assume that the speed of precession is not quasi-constant, but that it was for some reason greater in antiquity than in the present.

5.3.4 “Ptolemic”, “Almajest”

AbbreviATIONS
EXPLANATIONS

I know that it is inappropriate and ungrateful to engage in a polemic, or more “precisely” a “ptolemic”, with a “great old” scholar, but I must argue with Master Ptolemy! In my defence: Had Ptolemy not outed himself as the pope of the geocentric worldview, Giordano Bruno, who was at odds with him many centuries later, would not have been burned….

(You can be at odds with me; I’m just old and not a natural scientist. I can be persuaded because the debate is sweet, even if it is fiery for me. Of course, my argument is much less important than the debate of Giordano Bruno because I am not so convinced of my hypothesis as he was of his principles).

That’s all I said to the great old man:

“Dear Master Claudius!

I doubt you “accidentally” had overlooked the fact that there is such a significant discrepancy between your “own” precession parameters and Hipparchus’s. I do not believe you were not familiar with the differences in Spica coordinates measured in centuries.”

At first glance, this may sound like praise, but it is a serious objection.

Because of this “debate”, I researched the net and quickly came across some former “debaters” of late.

Many scholars have expressed doubts regarding Ptolemy’s data, especially regarding the data related to precession.

Some are more lenient. According to them, the multiple translations and copying, the slight differences in the Arabic numerals in the manuscript, which are easily confused, lead to distortions of content and highly disputable data in the Almagest, incredibly incorrect star coordinates. 

The more hard-line scholars consider the Almagest unprofessional, misleading treatise, a collection of errors and forgeries, thus proclaiming Ptolemy himself a “forger”.

It cannot be entirely without foundation that in his book “Crime of Claudius Ptolemy”, Robert R. Newton called Ptolemy simple a “criminal”.

And Dennis Rawlins called Ptolemy “the greatest forger of antiquity”. He gave the Almagest the nickname “ALMAJEST” in a witty play on words.

Gary David Thompson writes:

“In the material that has survived, Hipparchus does not use a single consistent coordinate system to denote stellar positions.  He inconsistently uses several different coordinate systems, including an equatorial coordinate system (i.e., declinations) and an ecliptic coordinate system (i.e., latitudes and longitudes).”

Duke’s “Ancient Declinations and Precession”

“…Dennis Rawlins recognised that “the locations specified by Ptolemy might be right ascensions… that the passage in Almagest 7.3 might be originally from Hipparchus”.

The summary of “PTOLEMIC”:
According to renowned scientists 
who have detailed examined the subject, 
it cannot be ruled out that some of 
Ptolemy’s stellar coordinates included in Almagest 
are not celestial ecliptic but rather 
celestial equatorial, RA coordinates.

(Celestial ecliptic: ecliptic longitude (Ecl. long.) and ecliptic latitude Ecl. lat.); others zodiacal. Celestial equatorial: hour angle, aka right ascension (RA) and declination (dec.), the celestial equivalent of the Earth’s meridian system, Earth’s longitude, and latitude; blogger’s note. See below).

5.3.3 Measuring of Precession

AbbreviATIONS
EXPLANATIONS

The most suitable stars for measuring the coordinates of the precession of the AEQ/VEQ points are those that are visible near the Ecliptic.

Spica is next to the Ecliptic, in the constellation of Virgo.

(In the middle of the goblet held in the left hand of the virgin sign, as shown in the photo above.)

Spica is easy to observe today on AEQ days because it appeared above the horizon when the Sun dipped below, and the sky darkened. This was not the case in ancient times. It is known that the coordinates of Spica in antiquity were measured primarily indirectly through the coordinates of the moon. The reason for this is as follows:

In the centuries of Timocharis, Hipparchus and Ptolemy, the celestial point of the autumn equinox, the AEQ point, was virtually very close to Spica. Today, the AEQ point is further away from Spica, as the photo above shows. Around the AEQ day, the Sun is also close to the AEQ point in the sky. This means that Spica also appears close to the Sun around the date of the AEQ. Therefore, in the centuries above, around the AEQ day, Spica was not visible to the naked eye because the Sun blinded the observer, as shown in the figure below.

Spica went under the horizon just before sunset and rose above the horizon just before sunrise. The following photo is darkened to show Spica just above the green line of the horizon and the Sun just on the horizon. (Of course, you can’t look below the horizon, only Stellarium allows you to do that.)

Both photos above were shot by the blogger with Stellarium at Sunrise on AEQ day of 128BC, in Alexandria, Egypt.

Fortunately, the full moon is just opposite the Sun. So, the coordinates of the Sun can be determined easily by measuring the coordinates of the moon. This was a usual procedure in antique astronomy.

Consequently, the simultaneity of the AEQ day and the full moon day could play an essential role in measuring the celestial position of the Spica. Note: Of course, the relative coordinates of Spica and the other stationary observable stars near the ecliptic plane (Alpha LEO; Alpha CMi, etc.) also supported the determination of the coordinates of Spica.

Let us look at the years of measurement from this point of view.

It can be observed that in two of the measurement years mentioned (278BC (-279); 128BC (-127)), AEQ and the full moon coincided. But the currently hypothetical year AD138 was not such an AEQ & full moon year.

It looks likely that all three years of measurement had to be coincident AEQ & full moon years.

However, instead of the uncertain AD138, 
the year AD131 would have been more appropriate, 
as this is the closest AEQ & full moon year.

AD150 could also fit but is out of the question because it is already the year of publication of Ptolemy’s very long and earlier written work.

The photo below was taken on 24 September AD131, on the day of the AEQ, about 1 hour before sunrise, and shows the sky from Alexandria. The Sun is still below the horizon, marked by the horizontal green line, near the AEQ point, the intersection of the Ecliptic and the celestial equator. Spica is to see in the circular frame next to both the AEQ point and the Sun. The coordinates of Spica are shown in the list on the left of the photo. It can also be seen that Spica is just above the Sun, and it will rise slightly before the Sun but will not be directly observable due to the Sun’s blinding proximity. (Stellarium photo by the blogger.)

The following photo is a wide-angle view of the East-West sky on AD131 on 24 September, on the day of AEQ, at the same time as the photo above. The full moon is well visible above the horizon, near the symbol for the VEQ celestial point, the other intersection of the Ecliptic and the celestial equator. The full moon is positioned opposite the Sun but will soon dip below the horizon. The coordinates of Spica can be calculated indirectly from the coordinates of the full moon. (Stellarium photo by the author.)

Let us have a look at the Ecl. long. coordinates of Spica on the dates of measurings as we see it, on the possible dates of AEQ and full Moon coincidence:

Table 4.

The above Table 4. is based on the data of Stellarium. It shows the changing of the ecliptical longitudinal (Ecl. long.) coordinates of Spica. The ecliptical longitudinal coordinates are traditionally measured from the VEQ point’s longitude zero. That is why the coordinates of Spica (and not those of the AEQ point) are changing.

Table 4. tells us, too, that the Ecl. long. of Spica gradually “approached” the AEQ point, which is at 180° Ecl. long. This table plays an essential role in the following.

5.3.2 Precession Calculations

AbbreviATIONS
EXPLANATIONS

There are several ways to calculate the attributes (parameters) of precession from the astronomical data of Almagest.

This subsection seems to be a short digression, but I recommend reading it not because it is short but because it is relevant for what follows.

Hipparchus measured the length of the tropical year (solar year) as 365 1/4 days – 1/300 days or expressed others 365 days 5 hours 55 minutes (rounded, slightly shorter than the well-known 365 1/4 days).

Today’s figure for the tropical year is ~365.24219 days, i.e., 365 days, five h 48 m 45s.

He measured the length of the sidereal year, 365 1/4 days + 1/144 days, i.e., 365 days 6 hours 10 minutes.

Today’s figure for the sidereal year is longer than the tropical year by 20 min 24.5 s, ~365.256360 days, i.e., 365 days 6 hours 9 m 9,54s.

The parameters of the precession can be calculated from these data.

The 15-minute per year time difference between the tropical and sidereal years lengths corresponds to 1 day in 96 years (24/0,25=96), and the cycle time is 96*365.25 = 35,064 years.

It means round 1°/97.4 years (96*365,25/360= 97.4) angular velocity. Both parameters are very much imprecise. Namely, according to today’s measurements, the difference between the length of the tropical and sidereal years is not about 15 minutes but about 20 minutes. The 20 minutes results in a rounded 72 years per degree instead of 97.4, making the cycle time of 25.920 years mentioned above. 72*360=25.920.)

However, astronomers say that we cannot be sure that Hipparchus was aware of the possibility of calculating the cycle time from tropical and sidereal years.

Based on the fixed star coordinates of Hipparchus and Ptolemy, the parameters of precession are calculated as follows:

Hipparchus’ measuring comes from 128BC (-127), and Ptolemy’s probably from 138AD.

According to Almagest, in the 265 years between these two measurements, the ecliptic longitudinal (short Ecl. long.) angular rotation of the fixed star SPICA was 2°40′ = 2.67°. Therefore 265/2.67 = 99.25 years/degree.

Calculated in this way, the angular velocity of precession is 1°/99.25 years, and the cycle time is 35,730 years (99.25*360=35,730).

Based on this latter calculation, the literature states that according to Ptolemy and the Almagest, the angular velocity of precession is at least 1°/100 years, with a cycle time maximum of 36.000 years.

This, like the above calculation, is a wildly inaccurate figure, too.

According to today's measurements: 
angular velocity: 1°/71.6 years, 
cycle time: 25,776 years. 
The ancient error is around 38%.

However, it is also written in Almagest 
and generally accepted that 152 years elapsed 
between the measurements of Hipparchus and Timocharis and that 
Hipparchus determined an angular change of 
2° Ecl. long. over this 152 years. 
A 2° precession angular change over 152 years corresponds to a 
precession angular velocity of 1°/76 years and a 
cycle time of 27,360 years. 
This is a much more accurate result than that of Ptolemy. 
It is also close to today's values given above.

Despite this facts, the literature emphasises Ptolemy's 
cycle time of "up to 36,000 years" and 
generally ignores Hipparchus' much earlier and 
more accurate figure of 27,360 years! 

For me, it's very noticeable and disturbing that 
there is such a massive difference between the calculations 
based on the coordinates of Hipparchus and that of Ptolemy. 
This observation will soon become very important!

5.3 The Precession Objection

AbbreviATIONS
EXPLANATIONS

The precession objection is the most compelling of the above astronomical refutations to the possibility of a historical time insertion. So I will devote some posts to its examination. 

The objection is essential, so I will repeat it:

“If history were about 2.5 centuries shorter, there would have been about 3 degrees less angular rotation because the angular velocity of precession is constant to an excellent approximation. Three degrees would be too much of an error even for old historical measurements, ”

As told, it is almost a paradox!

Namely, we must assume that only the years of the Roman era are shifted back in time, while the AD years of Hipparchus’ lifetime should be considered correct. In other words, we should find an astronomical solution to solve this contradictory situation.

Familiarity with some elements of astronomy is essential in this part, so I am serving the description in several smaller “portions” in the hope that it will be more “digestible”.

First, I will briefly explain the essence of precession because, in my experience, relatively few people are well informed on the subject.

Since ancient times, astronomers have been able to determine the time and celestial position of Vernal Equinox (VEQ) and Autumnal Equinox (AEQ), the astronomical date and celestial points in the sky with sufficient accuracy.

The VEQ and AEQ points are the intersections of two well-known “virtual orbital curves”. They are the intersection points of the Sun’s elliptic orbit (as seen from the Earth in the ecliptic plane) and the celestial equator (the projection of the Earth’s equator onto the sky in the Earth’s equatorial plane).

Ancient astronomers considered these points of intersection, which are almost opposite each other in the sky, as fixed. They usually determined the position of planets, stars and constellations, the celestial coordinates of the latter, relative to the AEQ or VEQ point.

Hipparchus (Greek: Hipparchcos; BC190-BC120), the great ancient Greek mathematician-geographer-astronomer, is credited with the first description of the astronomical fact that the position of AEQ and VEQ in the sky relative to the fixed stars is not constant. According to many researchers, this phenomenon had been known before, for example, in Babylonia, but was generally neglected.

Hipparchus recognised that (according to the geocentric model) it is not only the Sun and the stars that orbit the Earth. For the observer on Earth, the celestial coordinates of the VEQ and AEQ points change relative to the virtually stable position of the fixed stars.

Both points wander around the ecliptic over a very long period, roughly 25.920 years. It is a motion alongside the constellations observable near the ecliptic plane but in the opposite direction to the celestial motion of the Sun. (The round 25.920 years cycle time is usually used, but the calculations and measurements differ slightly from this rounded value)

This phenomenon is called the precession of equinoxes, short precession.

Precession is the third form of Earth’s movement, besides the rotation of the Earth around its own axis and its orbit around the Sun.

We can say that the Earth’s axis, seen from the north but from a very great distance, rotates (like the axis of a spinning top) from east to west around the north pole of the ecliptic in about 25.920 years. During this time, the Earth’s axis of rotation slowly aligns with different stars. Currently, we see the North Pole Star (Polaris) near the extension of the Earth’s axis of rotation. This was not the case in the past and will not be the case in the distant future. So, in about 13 000 years, Earth’s axis of rotation will be aligned with the brightest star in the constellation Lyra, the fixed star Vega.

CTRL+click here to watch this highly accelerated video!

The phenomenon of precession is also one of the foundations of astrology, as the zodiac signs are the “wandering constellations” visible close to the ecliptic plane. The average time between adjacent zodiacal constellations is 25.920/12 = 2.160 years. The boundaries of the signs are not clearly defined. These years we are moving from the constellation of Pisces to Aquarius.

The above diagram clearly shows the ancient symbol of VEQ, ♈︎. In celestial coordinate systems, the VEQ point has been used as a reference point for a very long time, for as long ago as the VEQ point yet coincided with the starting point of the constellation Aries. In fact, the symbol ♈︎ is a simplified drawing of the “horns of Aries”. And, as I see, it resembles a renewal, an unfolding flower, a branching shoot, too. Because of a similar reason, the symbol of the AEQ point, opposite to the VEQ point resembles a balance ( Ω, underlined Greek omega) and symbolizes the constellation Libra. Both ancient symbols reveal the symmetry of duality.

On both, the VEQ day and the AEQ day of the year, the 24-hour solar day is divided into two equal parts, a 12-hour light day and a 12-hour dark night.

5.2 “Loophole” in Metonic Cycle

AbbreviATIONS
EXPLANATIONS

The Sun symbolises a powerful male deity who illuminates our day and forces upon us the darkness of night feared in ancient times. The Sun is difficult to look at in the “eye” because it blinds.

The Moon represents a gentle goddess who dimly illuminates the darkness of night, and we can look into her eyes without fear.

Although the Sun is the more significant life-giving celestial body, the Moon is the more exciting, the more attractive celestial phenomenon, “who” is constantly changing her “appearance”, changing her dress, like a lady. This is how the ancient observer saw it, and we can agree with him today.

I started this chapter with this mood picture because some (probably “boring” for most of you readers) calculations will follow soon.

The Metonic cycle is almost exactly 19 years, after which a given moon phase recurs within the astronomical year. (Relative to the day of a given astronomical phenomenon like the VEQ). The lunar month and the moon phases have initially been more significant in time representation and measurement than the solar year.

It is evident that observations of the “behaviours” of the Moon formed the basis of the early “lunar calendars”. 

The ancient Chinese also knew the Metonic cycle. Thus, in the traditional antique lunisolar calendar, the Chinese still calculate the changing date of the Lunar New Year (Spring Festival) mainly based on the phases of the Moon.

The existence of the 19-year Metonic cycle was already known to the Babylonians and was used to correct the length of their lunar calendar year. However, the cycle was named after Meton, an Athenian mathematician and astronomer who lived in the 5th century BC.

The Metonic cycle allows for the construction of a calendar in which 12 years consist of 12 lunar months and seven years consist of 13 lunar months so that the total of 19 years spans 6940 days.

Callipus later specified the length of the Metonic cycle to 6939.75 days.

Both the 6.940 days and the 6.939,25 days were applied in different ancient Greek lunar calendars to correct the length of the year.

We have also seen that the calculation of the Easter tables (computus) in the Julian calendar was also based on the Metonic cycle.

The falsehood of the time reckoning can only be astronomical, so astronomy had to be relied upon to confuse the AD time. Even in ancient times, astronomers knew very well that any calendar, as we would say today, is only a tool for earthly digital approximation and modelling of analogue celestial reality.

Throughout the ages, people have tried to adapt the calendar to the periodic movements of the celestial bodies, first and foremost the Moon.

For this reason, ancient astronomers did not work with the calendar but with the well-observed tropical years (solar year) and the synodic lunar months (the time between two successive, similar lunar phases).

However, as seen, the 220 years of insertion 
is not an integer multiple 
of the 19 years of the Metonic cycle. 
Nevertheless, we should examine what happens 
to a given lunar phase 
assuming of insertion of 220 years! 

* The length of the tropical year as measured today: 365.24218967 days. 
* The synodic lunar month as measured today: 29.53058872 days. 
(The measured values vary slightly with time.)

The Metonic cycle compares 19 tropical years with the length of 235 synodic lunar months. This interval was transparent and relatively easy to measure in ancient times. Of course, the data differed slightly from current values; we know this, for example, from the precise dates of the old Chinese Taichu calendar.

Based on the above data, the 19 tropical years today correspond to 6939.60160393 days. The duration of the 235 synodic lunar periods is 6939.68834920 days.

Compared to the 19 tropical years, the Lunar phase delay today: is 0.08674547 days. (2h 5′) So, the Metonic cycle is a little inaccurate!

This inaccuracy makes 1.004421232 days, based on 220 years offset.

Very accurately, one day lunar phase time difference, 
in the case of 220-year time offset 
forwards or backwards. 
An astronomical time difference, 
comparing a specific event in the astronomical year, 
such as VEQ.

In the case of a forward jump (omission) of 220 years, it means a delay of the lunar phase by one day.

In the case of a backward jump (insertion) of 220 years, it means an advance of the lunar phase by one day.

As mentioned above, the timing of the phases of the Moon cannot be determined precisely with the naked eye.

Furthermore, the timing of celestial events, on average, slowly recedes in the Julian calendar and additionally “jumps back and forth” due to leap years.

The above three inaccuracies are superposed, added together, or subtracted.

In the case of a 220-year shifting backwards in the Julian calendar, a given lunar phase is on average 1.7 days ahead. Two hundred twenty years earlier, a given new moon occurs on a later but slightly different date from the average delay in the Julian calendar. We have already seen, for example, that the first new Moon of 45BC occurred almost quite exactly two calendar days later than the first new Moon of AD176.

To sum up: 
The above slight inaccuracy of the Metonic cycle 
explicitly supports the hiding of the insertion of 220 years. 
If 220 years were inserted, all historically recorded 
lunar phases would have been transformed 
into a similar lunar phases 220 years earlier. 
But the lunar phases remained almost precisely 
on their original astronomical day, 
so it wasn’t easy to detect the insertion! 
It was especially challenging to recognise the insertion 
because of the inaccuracy of the calendars.

To sum up: The above slight inaccuracy of the Metonic cycle explicitly supports the hiding of the insertion of 220 years. If 220 years were inserted, all historically recorded lunar phases would have been transformed into 220 years earlier similar lunar phases. But the lunar phases remained almost precisely on their original astronomical day, so it wasn’t easy to detect the insertion! It was challenging to recognise the insertion because of the inaccuracy of the calendars.

So, the slight inaccuracy in the Metonic cycle opened a ‘loophole’ to insert the 220 years in a way that is difficult to recognise.

In addition, at most, only a few astronomers could have wondered precisely on which calendar date a given lunar phase could have fallen 220 years earlier.

Nor have I found any reference in the literature to this particular property of the 220 years, that 220 years are associated with a moon phase shift of precisely one astronomical day.

5. FEASIBILITY of 220-YEAR SHIFT

AbbreviATIONS
EXPLANATIONS

The word feasibility in this context expresses achievability, possibility, and reasonableness simultaneously. In this post, I address the above astronomical counterarguments that only seemingly rule out the possibility of inserting 200-300 years into the AD era.

We show why the exclusion of insertion does not work.

Of course, the insertion of 220 years seems unacceptable based on the astronomical counterarguments given above, as the insertion of 200, 247 and 297 years did.

For 220 is not divisible by 28 (solar cycle) or 19 (Metonic cycle), but it is divisible by at least 4 (the leap year cycle in the Julian calendar).

At first glance, 224 years would be more appropriate because 224 is a multiple of the solar cycle, 8*28=224.

The closest number of insertable years that would correspond to the Metonic cycle and could be inserted would be 11*19=209 years or 12*19=228 years.

By analysing the Jewish calendar and the Metonic cycle, I show that precisely 220 years is the period whose insertion in the AD time reckoning is “hard-to-detect” for astronomical and calendrical reasons.

As a further issue, according to astronomers, Hipparchus determined the positions of many fixed stars in his star catalogue with reasonable accuracy.

During the years Hipparchus lived, these fixed stars could be seen in the sky in good approximation to the position he indicated.

Therefore, we must assume that Hipparchus lived between 190 BC and 120 BC, as we know it today.

Therefore, we could assume that only the years of the Roman era are shifted back in time, while the AD years of Hipparchus’ lifetime can still be considered correct.

It is almost a paradox! 
Therefore, temporarily 
– despite the 220 years resulting in the HEUREKA post – 
it still seemed impossible to me, 
that 220 years of history could have been inserted.

The “legend of the Star of Bethlehem” helped me overcome this mental deadlock.

Kepler guessed that this legend is linked to a conjunction of Jupiter and Saturn.

In antique astronomy and stargazing, the celestial movements of the planets Jupiter and Saturn and the conjunction of these planets were of fundamental importance. The Jupiter-Saturn conjunction was called the “grand conjunction” in astronomy and the “great chronocrator” (meaning the Time-Lord marking the start of a new cycle of world affairs) in astrology.

The cycle time of the Jupiter-Saturn conjunction 
is almost exactly 20 years. (19.86 years) 
This seemed to confirm my suspicions, 
the possibility of 220 years being inserted 
since it is obvious to me that 
an error in the AD time calculation 
can only be an integer multiple of 20 years, 
and 11*20 = 220.

In my opinion, this fact would have been considered in any case when falsifying the time reckoning or subsequently sanctifying an error! Without taking this period into account, it would have been too easy to detect the mistake afterwards.

So, considering the 20-year cycle of the Jupiter-Saturn conjunction was inevitable.

Inevitably. Regardless of whether the legend of the Star of Bethlehem is really related to J-S conjunction or whether it is merely Kepler’s conjecture! Even more so because Kepler only suspected that the Jupiter-Saturn conjunction had generated some bright celestial phenomenon, such as a comet, in the year of Jesus’ birth.

However, the 20-year cycle of the J-S conjunction is also an “additional boundary condition” that may make it impossible to insert 220 years.

This means that the number of insertable years must not only be divisible by 19 but also by 20.

I would say that it was at this point that I became excited by the task of astronomically verifying my earlier historical conjecture.

The next step is to examine whether 
the insertion of 220 fictitious years into history 
was astronomically possible at all. 
That is, whether the insertion could remain 
astronomically "difficult to recognise".