Among the refutations of the theories about the falsehood of the AD time, I agree with the statement that the number of years to be inserted must be divisible by 4. Otherwise, the long-established rhythm of Julian’s leap years would be upset. Even the layman could have quickly realised this mistake.
However, the assertion that the number of years to be inserted must be divisible by 28 (the number of years in the solar cycle) is not acceptable, as far as I see.
My reason is that the 28-year solar cycle is only a feature of the Julian calendar.
The solar cycle is not fulfilled even for the Gregorian calendar, only a tiny variation of the Julian calendar!
If someone thinking according to the Julian calendar wants to insert 2-3 centuries, then, of course, to keep the order of the seven days of the week, he would have to consider the solar cycle. So that only annual intervals, which are divisible by 28, would come into question for insertion.
However, Friday 14 Nisan, (The Friday before the Jewish Passover, Pascha, the “Jewish Easter”) could not have been changed by the insertion. This date was engraved in the memory of believers as the date of Jesus’ crucifixion. Consequently: to keep Friday on the 14th of Nisan, ones should think and do according to the Jewish calendar.
The Jewish calendar is an old and essentially religious calendar. Its primary use is to calculate the dates of religious holidays, but it is also used sometimes in civil life, for example, to estimate agricultural dates. It is considerably more complicated than the Julian calendar because it is “lunisolar”, i.e., it can adapt to the course of the moon and the sun simultaneously over a long period. It achieves this by defining six years of different lengths (353, 354, 355, 383, 384 and 385 days). Although the subject is fascinating, only a single feature of the Jewish calendar is of interest to us now, so we will only deal with it in the following.
Therefore, the structure of the Jewish calendar differs significantly from that of the Julian calendar. This means that other rules apply for the possibility of insertion of a period than in the Julian calendar.
The periodicity of Nisan 14 Friday is not evident in such a complicated calendar. Examining the Jewish calendar shows that Nisan 14 Friday occurs mainly only 2 to 3 times in a decade.
We want to investigate whether it allows inserting precisely 220 years, so the situation is simple.
We need to think in perspective because we are looking for the original state in a later period. So, we “only” should determine whether, by shifting the years between AD26 and AD36 (the possible period of the date of Jesus’ crucifixion according to our current knowledge) to another period 220 years later, in what years the date Nisan 14 would fall on a Friday if any.
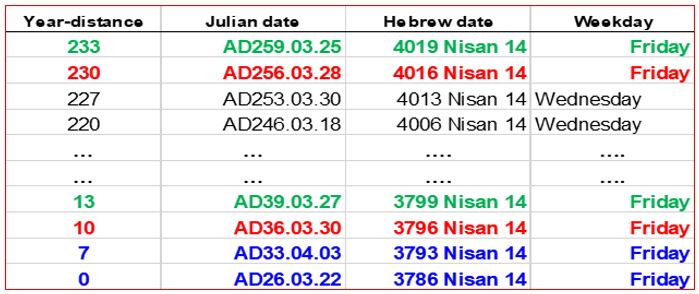
Table 3. (Based on Fourmilab’s calendar converter )
In the blue year-rows, the 14th of Nisan falls on a Friday, but they do not have a fitting pair of Fridays 220 years later. Therefore, the black year-rows are irrelevant because the 14th of Nisan does not fall on a Friday 220 years later.
The green and red lines are 220 years apart and form Friday pairs of the 14th Nisan.
According to today’s view, only AD33 or AD36 comes into question, so the green rows can be neglected.
The conclusion based on Table3 is: In AD256, the backward shift of the date Nisan 14 Friday by 220 years was possible according to the Jewish calendar. So, it was not necessary to follow the 28-day rule of the Solar Cycle to maintain the order of the seven days of the week during the insertion. The year of Jesus' crucifixion may have been shifted back alongside the time scale by 220 years.
Note:
The Friday can remain on Nisan 14 at inserting of 200 years, too (a’ la Hunnivari). (Nisan 14 falls on a Friday in AD236).
From this, I conclude that the insertion of the 220 years of my hypothesis may have been attempted in two independent tranches of 20 and 200 years, probably at different times.
